Spatial causal inference in the presence of unmeasured confounding and interference
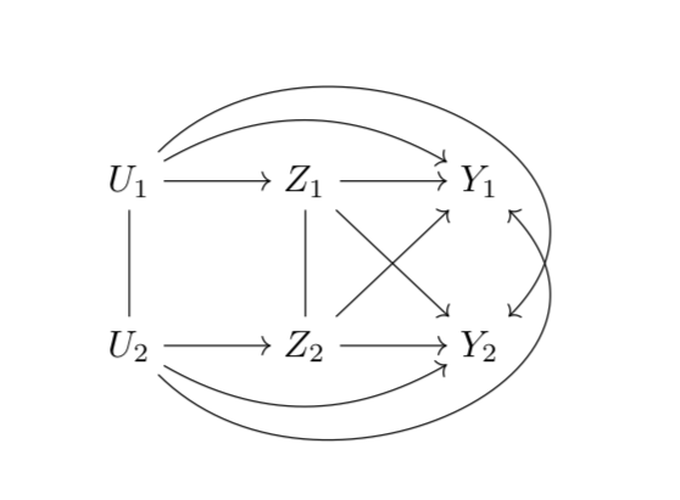 Causal and statistical relationships among a confounder, exposure, and outcome.
Causal and statistical relationships among a confounder, exposure, and outcome.
Spatial causal inference in the presence of unmeasured confounding and interference
Abstract
This manuscript bridges the divide between causal inference and spatial statistics, presenting novel insights for causal inference in spatial data analysis, and establishing how tools from spatial statistics can be used to draw causal inferences. We introduce spatial causal graphs to highlight that spatial confounding and interference can be entangled, in that investigating the presence of one can lead to wrongful conclusions in the presence of the other. Moreover, we show that spatial dependence in the exposure variable can render standard analyses invalid, which can lead to erroneous conclusions. To remedy these issues, we propose a Bayesian parametric approach based on tools commonly-used in spatial statistics. This approach simultaneously accounts for interference and mitigates bias resulting from local and neighborhood unmeasured spatial confounding. From a Bayesian perspective, we show that incorporating an exposure model is necessary, and we theoretically prove that all model parameters are identifiable, even in the presence of unmeasured confounding. To illustrate the approach’s effectiveness, we provide results from a simulation study and a case study involving the impact of sulfur dioxide emissions from power plants on cardiovascular mortality.