Abstract

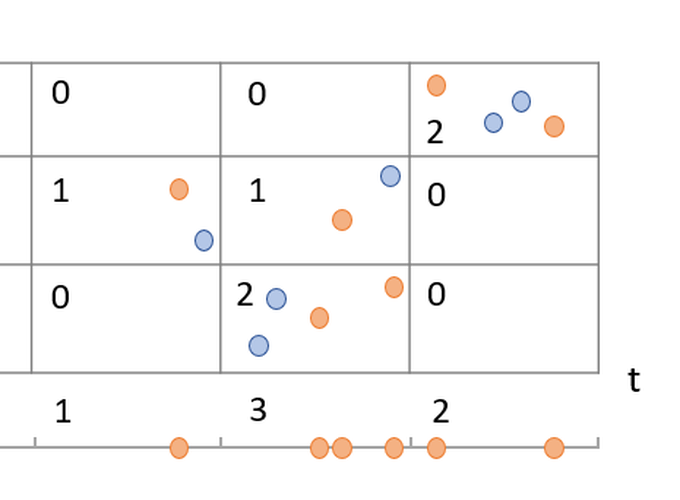
The Hawkes process, a self-exciting point process, has a wide range of applications in modeling earthquakes, social networks and stock markets. The established estimation process requires that researchers have access to the exact time stamps and spatial information. However, available data are often rounded or aggregated. We develop a Bayesian estimation procedure for the parameters of a Hawkes process based on aggregated data. Our approach is developed for temporal, spatio-temporal, and mutually exciting Hawkes processes where data are available over discrete time periods and regions. We show theoretically that the parameters of the Hawkes process are identifiable from aggregated data under general specifications. We demonstrate the method on simulated data under various model specifications in the presence of one or more interacting processes, and under varying coarseness of data aggregation. Finally, we examine the internal and cross-excitation effects of airstrikes and insurgent violence events from February 2007 to June 2008, with some data aggregated by day.